Messsysteme
Rundheitsmessgerät
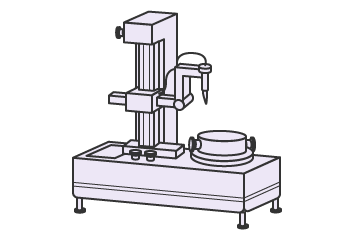
Dieses Messgerät kann Geradheit, Rundheit, Zylindrizität, Parallelität, Rechtwinkligkeit, Koaxialität, Rundlauf und Gesamtrundlauf messen. Im Allgemeinen sind Rundheitsmessgeräte mit einem Drehtisch ausgestattet und verwenden einen Taststift, der die Messobjekte berührt, um verschiedene geometrische Eigenschaften zu messen.
3D-Koordinatenmessgerät
3D-Koordinatenmessgeräte können verschiedene geometrische Eigenschaften für Formtoleranz, Ausrichtungstoleranz und Lagetoleranz messen.
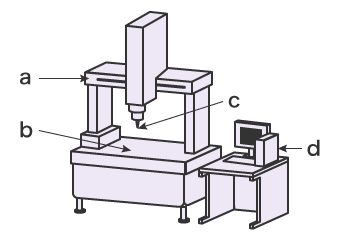
- a
- Bewegliche Brücke
- b
- Objekttisch
- c
- Auslösetaster
- d
- Steuerung
Ein taktiles 3D-Koordinatenmessgerät erfasst dreidimensionale (X-Y-Z-) Koordinaten, wenn der Bediener den Messpunkt oder die Messlinie des Messobjekts mit dem Kugeltaststift an der Spitze des Messtasters angibt. Da die Elemente (Geraden, Ebenen, Kreise, Kugeln usw.) aus einem Satz von erfassten Koordinaten berechnet werden, kann ein 3D-Koordinatenmessgerät neben den Längen komplexer stereoskopischer Objekte auch Winkel, Positionsbeziehungen zwischen Elementen, Profile und geometrische Abweichungen präzise messen.

Stationäre Modelle waren zwar früher gebräuchlicher, sie erforderten jedoch eine Temperaturregelung, es gab Einschränkungen bei der Wahl des Aufstellungsraums und die Größe des Messobjekts orientierte sich an der Größe des Messgerätes. Die Bedienung war außerdem kompliziert und erforderte sehr qualifizierte Bediener.
In den letzten Jahren wurden mobile, kompakte Arten von 3D-Koordinatenmessgeräten mit handgeführten Messtastern entwickelt, wodurch viele Probleme der stationären Modelle gelöst wurden.
- Info-Kasten
-
- Methode der kleinsten Quadrate
-
Auch wenn die für die Messung notwendigen Punkte mit dem Taststift eines 3D-Koordinatenmessgeräts festgelegt werden, kann die Form, die durch alle diese Punkte geht, immer noch von der wahren Form abweichen. In diesem Fall wird nach der Messung die Methode der kleinsten Quadrate angewendet.
Nehmen wir zum Beispiel einen Kreis: Ein Kreis wird durch Berechnen des Mittelwertes gebildet, der die Summe der Abweichungsquadrate in radialer Richtung jedes Messpunktes minimiert.
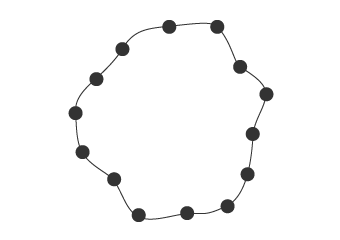
Messpunkte 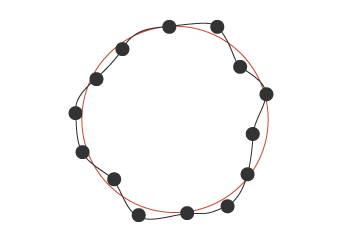
Form erzeugt durch die Methode der kleinsten Quadrate
(rote Linie)